Новая веха квантовой симуляции? Квантовый компьютер показал «невидимые» силы между частицами

Знаете, физика — штука занятная. Мы вроде бы живем в понятном мире стульев, столов и котиков, но копни глубже — и там целый «зоопарк» элементарных частиц. Электроны, позитроны, всякие там кварки… Все это взаимодействует, создавая силы, которые, собственно, и держат наш мир вместе. И чтобы понять, как все это работает, ученые строят модели. Самая успешная из них — Стандартная модель. Звучит солидно, правда?

Но вот незадача: описать поведение этих частиц и полей — задачка со звездочкой. Теория есть, а вот просчитать все нюансы на практике невероятно сложно. Представьте, что пытаетесь предсказать погоду не на завтра, а на год вперед, учитывая движение каждой молекулы воздуха. Примерно так же обстоят дела с квантовыми полями. Тут даже самые навороченные суперкомпьютеры часто пасуют. А ведь так хочется разгадать все секреты Вселенной!

Так в чём же загвоздка? Почему так трудно?

Позвольте объяснить по-простому. Большинство компьютеров, и классические, и многие квантовые, мыслят двоично: есть сигнал — нет сигнала, ноль — единица. Это отлично работает для многих задач. Но квантовые поля, особенно те, что отвечают за силы (вроде электромагнетизма), — штуки более хитрые. У них есть не только «сила», но и «направление». Они могут быть слегка «возбуждены» или очень сильно.

Пытаться описать такое поле, используя только нули и единицы, — это как пытаться нарисовать полноцветную картину, имея в руках лишь черный и белый карандаши. Можно, конечно, извернуться, разбить все на крошечные точки… но это жутко неудобно и требует уйму ресурсов. Вычисления становятся такими громоздкими, что даже квантовые компьютеры, основанные на битах (кубитах), сталкиваются с проблемами.

А что, если бы у нас было больше «красок»?

И вот тут на сцену выходят ребята из Инсбрукского университета и Университета Ватерлоо. У них появилась идея: а что, если использовать квантовые системы, которые могут находиться не только в двух состояниях (0 или 1), а в большем количестве? Скажем, в трех, четырех, или даже пяти! Такие «многозначные» квантовые биты называют кудитами.

Команда Мартина Рингбауэра в Инсбруке как раз построила такой не совсем обычный квантовый компьютер. А теоретическая группа Кристин Мушик в Ватерлоо разработала специальный алгоритм, как на этом «железе» можно моделировать взаимодействия частиц. Фишка в том, что кудиты позволяют представить сложные квантовые поля гораздо естественнее. Без необходимости дробить их на бесконечные нули и единицы.

«Это делает расчеты куда эффективнее», — поясняет Михаэль Мет, один из авторов исследования. И это не просто слова. Им удалось сделать то, что раньше было крайне затруднительно.

От прямой линии к реальному миру (почти!)

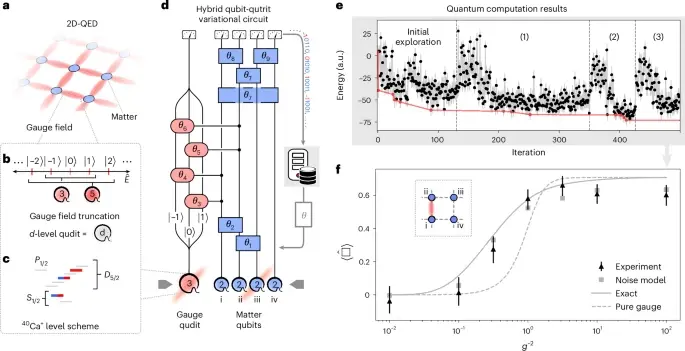
Помните, я говорил про электромагнитную силу? Это часть теории, называемой квантовой электродинамикой (КЭД). Пару лет назад, в 2016-м, ученые уже смогли смоделировать на квантовом компьютере рождение пар частица-античастица (например, электрона и позитрона). Но была одна хитрость: частицы могли двигаться только по прямой линии, в одном измерении. Это, конечно, интересно, но в реальном мире все происходит в трех измерениях.

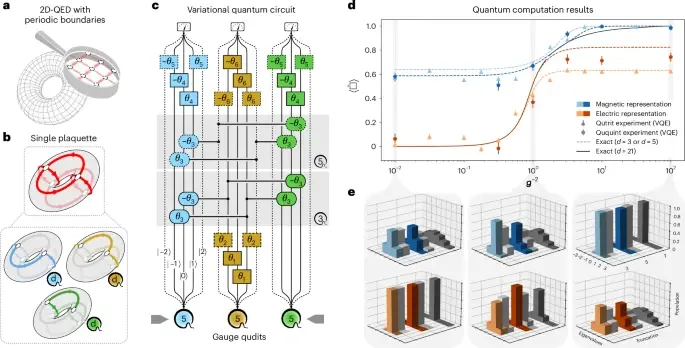
Так вот, новое достижение — это симуляция КЭД уже в двух пространственных измерениях! Казалось бы, всего одно измерение добавили, а какая разница! «Раньше частицы были словно на привязи, могли двигаться только вперед-назад», — говорит Мушик. Теперь же они могут перемещаться по плоскости.

И тут проявилось кое-что важное. «Мы увидели не только сами частицы, но и магнитные поля между ними», — объясняет Рингбауэр. А эти поля могут возникнуть, только если у частиц есть свобода движения хотя бы в двух измерениях. Это уже гораздо ближе к тому, как все устроено на самом деле. Маленький шаг для симуляции, но огромный — для понимания природы!

Что дальше? Заглядывая за горизонт

Конечно, два измерения — это еще не три, и КЭД — это только часть Стандартной модели. Но это очень важный шаг. Эта новая техника, использующая кудиты, открывает двери для моделирования куда более сложных вещей.

Например, сильное ядерное взаимодействие. Это та сила, которая склеивает протоны и нейтроны в ядрах атомов. Понять ее до конца — одна из больших задач современной физики. И есть надежда, что с помощью таких вот продвинутых квантовых симуляций удастся пролить свет на ее тайны. Достаточно добавить еще немного кудитов — и можно будет замахнуться не только на 3D-модели, но и на эту самую могучую силу природы.

«Мы очень воодушевлены тем, как квантовые компьютеры могут помочь в изучении этих захватывающих вопросов», — делится Рингбауэр. И, честно говоря, его можно понять. Похоже, у нас появляется новый мощный инструмент, чтобы задавать Вселенной самые каверзные вопросы. Кто знает, какие еще сюрпризы ждут нас за поворотом, когда мы научимся лучше «разговаривать» с квантовым миром на его собственном языке?