Квантовая запутанность в частотной области: новый подход к квантовой информации

В мире квантовой механики, где частицы ведут себя непредсказуемо и загадочно, ученые постоянно ищут новые способы понять и использовать эти странные свойства. Одной из таких загадок является квантовая запутанность — явление, при котором две частицы связаны невидимой нитью, независимо от расстояния между ними. Изменение состояния одной частицы мгновенно отражается на другой, словно они танцуют в унисон, подчиняясь таинственной квантовой мелодии.

Долгое время ученые изучали запутанность в различных степенях свободы, таких как поляризация, направление движения, орбитальный момент и временные интервалы. Теперь же исследователи из Южной Кореи сделали новый шаг, переместив танцпол фотонов в частотную область.

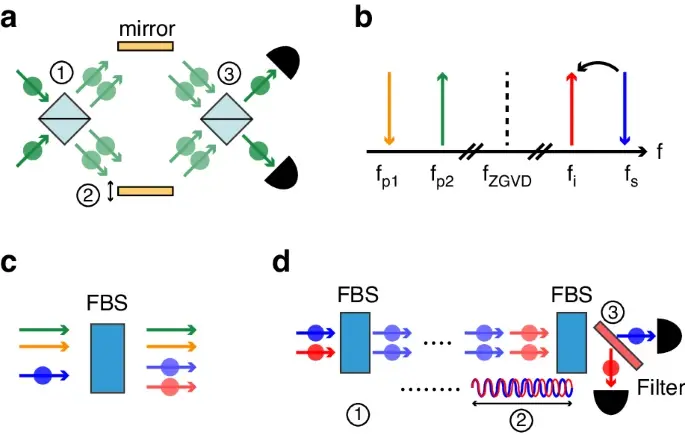
Представьте себе два фотона, отличающихся только цветом, подобно красному и синему лучу. Ученые создали частотный делитель луча, который с 50%-ной вероятностью превращает красный фотон в синий и наоборот. Это похоже на обычный делитель луча, только вместо пространственных путей он разветвляет пути в цветовом спектре.

Пропустив пару запутанных фотонов через такой делитель, исследователи получили NOON-состояние, которое представляет собой суперпозицию двух возможностей: либо оба фотона красные, либо оба синие.

Затем ученые заставили NOON-состояние снова пройти через частотный делитель и наблюдали за интерференцией — явлением, при котором волны света складываются или вычитаются, создавая узоры. Оказалось, что интерференционная картина NOON-состояния имеет вдвое большую разрешающую способность, чем у одиночных фотонов. Это открывает новые возможности для квантовой метрологии — науки о предельно точных измерениях.

Более того, новый интерферометр обладает невероятной стабильностью. Так как оба фотона путешествуют по одному и тому же волокну, их фазы меняются синхронно, что компенсирует любые внешние возмущения. Это делает интерферометр практически нечувствительным к вибрациям, температурным колебаниям и другим помехам.

Исследователи уверены, что их работа — это лишь первый шаг в освоении частотной области квантовой механики. Они видят перспективы в создании высокоразмерных квантовых состояний, которые могут быть использованы для создания квантовых компьютеров, защищенных каналов связи и сверхчувствительных датчиков.