Ещё шаг к квантовому превосходству? Ученые достигли универсального управления четырьмя кубитами

Статья, опубликованная в журнале Nature Nanotechnology, знаменует собой значительный прорыв в области квантовых вычислений. Учёным удалось достичь полного когерентного контроля над четырьмя кубитами, реализованными на основе спинов электронных пар в массиве квантовых точек из германия. Это открытие не только демонстрирует впечатляющий уровень управления квантовой системой, но и указывает на перспективность использования подобных систем для построения масштабируемых квантовых компьютеров.

Квантовые точки: миниатюрные хранилища информации

В основе эксперимента лежат квантовые точки — крошечные полупроводниковые структуры, в которых электроны заперты в ограниченном пространстве. Поведение электронов в этих «клетках» подчиняется законам квантовой механики, что позволяет использовать их в качестве кубитов — фундаментальных элементов квантовых компьютеров. В данном исследовании использованы кубиты, кодированные в состояниях синглет-триплет — суперпозиция спиновых состояний пары электронов. Выбор данной системы обусловлен её потенциальными преимуществами перед другими типами кубитов: полностью электрическое управление за счёт применения импульсов напряжения, отсутствие необходимости в микроволновом облучении, что снижает потери энергии и улучшает когерентность.

Сложности масштабирования: от единиц к множеству

Создание квантового компьютера — задача невероятно сложная. Основные трудности связаны с необходимостью когерентного управления всё большим количеством кубитов, а также с минимизацией ошибок, неизбежных при работе с квантовыми системами. Хотя ранее были достигнуты успехи в управлении небольшими группами кубитов (до шести), масштабирование до больших массивов оставалось большой проблемой. Создать полноценную квантовую систему с множеством взаимодействующих кубитов крайне сложно из-за ограничений размеров и геометрических параметров наноразмерных устройств, а также из-за необходимости работы в криогенных условиях с высокочастотными электромагнитными полями. Исследование, описанное в статье, представляет собой важный шаг к преодолению этих сложностей.

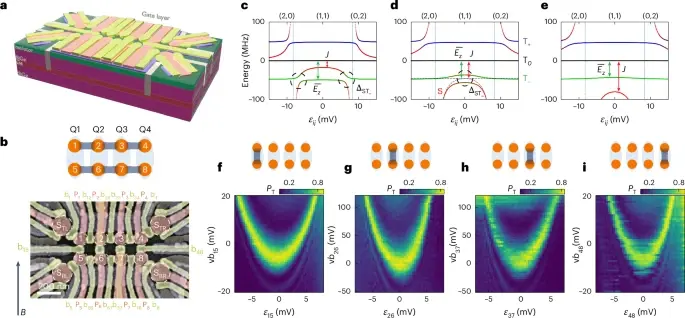
Достигнутые результаты: точность и взаимодействие

Учёным удалось создать двумерный массив из восьми квантовых точек, организованных в виде лестницы. В этой структуре были определены четыре кубита синглет-триплетного типа, и осуществлено их когерентное управление. Достигнутая точность впечатляет: средняя точность однокубитных операций достигла 99,49-99,84%, а точность реализации двухкубитных вентилей — 73-90%. Экспериментально продемонстрирована возможность генерации и распределения запутанности между кубитами в массиве. Удалось создать отдалённое запутанное состояние Белла с достоверностью 75%.

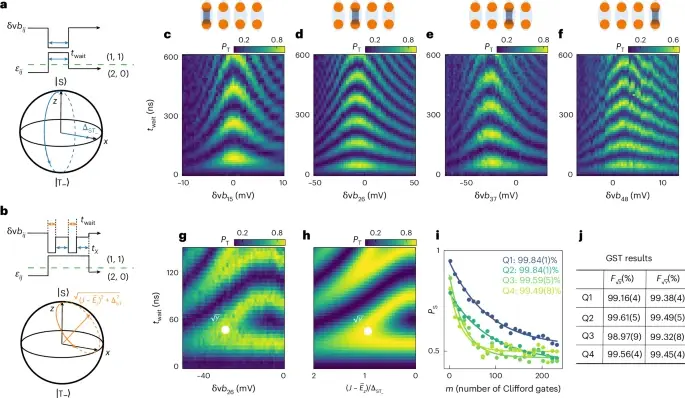
Дальнейшие перспективы: путь к масштабируемым системам

Результаты исследования указывают на перспективность использования кубитов синглет-триплетного типа в качестве конкурентоспособной платформы для построения квантовых компьютеров. Успешное масштабирование управления спинами в расширенных билинейных массивах стало более реалистичным. Дальнейшее повышение точности двухкубитных операций является ключевым фактором на пути к созданию отказоустойчивых квантовых вычислений. Авторы предполагают, что система может быть использована для моделирования сложных физических явлений, таких как квантовый магнетизм.

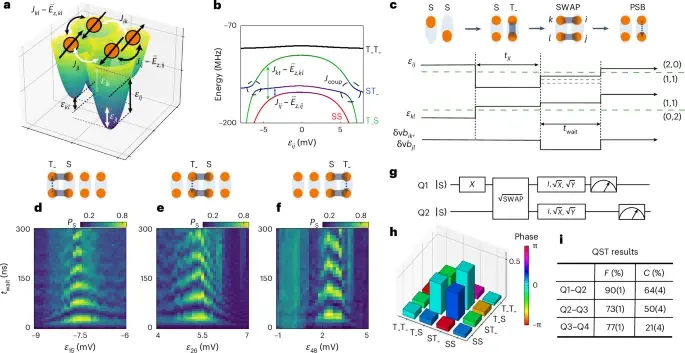
Заключение

Статья демонстрирует значительный прогресс в области квантовых вычислений. Управление четырьмя взаимодействующими кубитами, реализованное с высокой точностью, приближает нас к созданию масштабируемых квантовых компьютеров. Дальнейшее совершенствование технологии, ориентированное на улучшение точности и снижение ошибок, обеспечит создание практически применимых квантовых вычислительных устройств.